La ricorsione¶

Dove parliamo di procedure che si comportano come gatti che inseguono la loro coda

Definizioni ricorsive¶

Abbiamo visto che una funzione, una volta definita, può essere utilizzata al pari di ogni altro comando primitivo. È anche possibile che una funzione chiami sé stessa. In questo caso si dirà che la funzione è ricorsiva.

Nella matematica esistono diversi esempi di definizioni ricorsive ad esempio nel caso di potenze ad esponente naturale si può dire che:

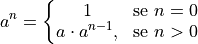
$a^n= \left\{ \begin{matrix} 1 & \mbox{se }n=0 \\ a \cdot a^{n-1}, & \mbox{se }n>0 \end{matrix} \right.$

Un altro classico esempio di ricorsione è la ricerca di una parola in un dizionario:

per la ricerca di una parola:
  apro a caso e leggo una parola a caso,
  se è la parola cercata:
    ho finito,
  se la parola che cerco viene prima di quella letta:
    eseguo la ricerca della parola a sinistra di quella letta
  altrimenti:
    eseguo la ricerca della parola a destra di quella letta.

Condizione di terminazione¶

Vediamo un altro esempio di definizione ricorsiva:

la scalinata di Giacobbe è:
  Un gradino seguito da una scalinata di Giacobbe

Quanti gradini ha? …

E se volessimo una scalinata un po” meno impegnativa?

Una scalinata di enne gradini è:
  uno scalino seguito da una scalinata di enne-1 gradini.

Oppure in una forma direttamente traducibile in un linguaggio di programmazione:

una scalinata di enne gradini è:
  se enne è uguale a 0: (la scalinata è) finita
  (altrimenti è) un gradino seguito da
  una scalinata di enne-1 gradini

Quest’ultima funzione presenta nella prima riga la verifica di una condizione. È la condizione di terminazione ed è importantissima per rendere funzionante la procedura, senza di questa la procedura continua all’infinito, o meglio finché non termina lo spazio disponibile nella memoria RAM e termina quindi con un errore.

Ricorsione non terminale¶

Negli esempi precedenti la chiamata ricorsiva è l’ultima istruzione eseguita della funzione. Queste sono dette funzioni ricorsive terminali e possono essere tradotte facilmente in un ciclo.

Ci sono anche funzioni che prevedono dei comandi da eseguire dopo la chiamata ricorsiva, in questo caso funzioni anche molto brevi possono presentare un comportamento molto complesso. Vediamo due esempi di funzioni ricorsive non terminali. Per la prima realizziamo un’astrazione a partire da un elemento naturale: un albero.

Un albero è formato da un tronco seguito da alcuni rami. Se seghiamo un ramo e lo raddrizziamo possiamo notare che assomiglia molto ad un albero: ha un primo segmento, una specie di tronco, seguito da alcuni rami, ognuno di questi rami assomiglia a sua volta ad un albero. Potremmo dire che un albero è un tronco con sopra alcuni alberi. Decidiamo una condizione di terminazione: se l’albero è più piccolo di 2 allora è fatto. Decidiamo anche che nel nostro albero da tutte biforcazioni partono due rami uguali e che l’angolo tra questi due rami è di 90 gradi. La funzione in un linguaggio intermedio potrebbe essere:

un albero di una certa lunghezza è:
  se la lunghezza è minore di 2: finito... altrimenti:
  disegno il tronco con quella lunghezza,
  giro a sinistra di 45 gradi
  disegno un albero di metà lunghezza,
  giro a destra di 90 gradi
  disegno un albero di metà lunghezza,
  rimetto a posto tartaruga

Da notare che l’ultima riga è fondamentale: alla fine del disegno di un albero (di ogni sottoalbero) tartaruga deve essere riportata nella posizione iniziale.

La traduzione in Python diventa:

import pygraph.pyturtle as tg

def albero(lung):
    if lung < 2: return   # condizione di terminazione
    tina.forward(lung)
    tina.left(45)
    albero(lung/2)        # prima chiamata ricorsiva
    tina.right(90)
    albero(lung/2)        # seconda chiamata ricorsiva
    tina.left(45)            # tartaruga
    tina.back(lung)          # è rimessa a posto

piano = tg.TurtlePlane()
tina = tg.Turtle()
tina.left(90)
tina.up()
tina.back(100)
tina.down()
albero(100)
piano.mainloop()

Nota

Quando creiamo una tartaruga possiamo assegnare dei valori ai suoi attributi quindi le istruzioni da tina = tg.Turtle() a tina.down() possono essre sostituite da un’unica istruzioni che risulta anche più comprensibile: tina = tg.Turtle(d=90, y=-100)

Dove d sta per direction e y sta pe la coordinata y della sua posizione.

Ogni albero ha un caratteristico angolo tra i rami, possiamo aggiungere questo parametro alla nostra funzione:

import pygraph.pyturtle as tg

def alberobin(lung, angolo):
    if lung < 2: return
    tina.forward(lung)
    tina.left(angolo)
    alberobin(lung/2, angolo)
    tina.right(2*angolo)
    alberobin(lung/2, angolo)
    tina.left(angolo)
    tina.back(lung)

piano = tg.TurtlePlane()
tina = tg.Turtle(d=90, y=-100)
albero(100, 60)
piano.mainloop()

E possiamo così disegnare alberi di specie diverse. Un albero ha anche la caratteristica di avere lo spessore dei rami che diminuisce man mano che ci si allontana dalle radici. Possiamo modificare l’attributo width per rendere più realistici i nostri alberi:

import pygraph.pyturtle as tg

def alberobin(lung, angolo):
    if lung < 2: return
    tina.setwidth = lung/5
    tina.forward(lung)
    tina.left(angolo)
    alberobin(lung/2, angolo)
    tina.right(2*angolo)
    alberobin(lung/2, angolo)
    tina.left(angolo)
    tina.back(lung)

piano = tg.TurtlePlane()
tina = tg.Turtle(d=90, y=-100)
alberobin(100, 60)
piano.mainloop()

Diversi alberi¶

Nello scrivere la funzione albero sono state fatte molte scelte che rendono piuttosto rigida la funzione stessa, possiamo parametrizzare diversi elementi:

il rapporto tra lunghezza e larghezza dei rami,
il decremento del sottoalbero di sinistra,
che può essere diverso dal decremento del sottoalbero di destra.

Ovviamente non basta aggiungere i parametri nell’intestazione della funzione, ma bisogna anche che tutte le chiamate ricorsive abbiano il giusto numero di parametri:

import pygraph.pyturtle as tg

def alberobin(lung, angolo, larg, decsx, decdx):
    if lung < 2: return
    tina.width = lung*larg
    tina.forward(lung)
    tina.left(angolo)
    alberobin(lung*decsx, angolo, larg, decsx, decdx)
    tina.right(2*angolo)
    alberobin(lung*decdx, angolo, larg, decsx, decdx)
    tina.left(angolo)
    tina.back(lung)

piano = tg.TurtlePlane()
tina = tg.Turtle(d=90, y=-100)
alberobin(100, 60, 0.1, 0.8, 0.6)
piano.mainloop()

Modificando i parametri possiamo disegnare alberi di un gran numero di specie diverse… I disegni ottenuti risultano un po” innaturali. Nel mondo reale molte cause provocano delle differenze di accrescimento dei vari rami, possiamo aggiungere un elemento di casualità alla crescita dei vari rami, una variazione casuale rispetto alla lunghezza passata come parametro.

import pygraph.pyturtle as tg
import random

def alberobincas(lung, angolo, larg, decsx, decdx, caos):
    if lung < 2: return
    var = int(lung*caos)+1
    l = lung - var + random.randrange(2*var)
    tina.width = lung*larg
    tina.forward(lung)
    tina.left(angolo)
    alberobincas(l*decsx, angolo, larg, decsx, decdx, caos)
    tina.right(2*angolo)
    alberobincas(l*decdx, angolo, larg, decsx, decdx, caos)
    tina.left(angolo)
    tina.back(lung)

piano = tg.TurtlePlane()
tina = tg.Turtle(d=90, y=-100)
alberobincas(100, 60, 0.1, 0.8, 0.6, 0.3)
piano.mainloop()

Degli altri alberi possono essere realizzati a partire da alberi ternari:

def alberoter(lung, angolo):
    if lung < 2: return
    tina.width = lung/5
    tina.forward(lung)
    tina.left(angolo)
    alberoter(lung/2, angolo)
    tina.right(angolo)
    alberoter(lung/2, angolo)
    tina.right(angolo)
    alberoter(lung/2, angolo)
    tina.left(angolo)
    tina.back(lung)

L’approfondimento è lasciato a chi è interessato.

Il fiocco di neve¶

Negli alberi la funzione è trasparente, non modifica la posizione di Tartaruga: Tartaruga viene riportata dove era stata presa. C’è un’altra famiglia di linee ricorsive che si comportano come segmenti: prendono Tartaruga in un posto e la spostano in un altro. Un famoso esempio di queste linee è la curva di Koch:

livello 0: ______________

                 /\
livello 1:      /  \
           ____/    \____

               __/\__
livello 2:     \    /
           _/\_/    \_/\_

A livello zero la curva di Koch è un segmento, ad ogni aumento di livello ogni segmento è sostituito da un segmento con la stessa lunghezza e con una protuberanza al centro.

import pygraph.pyturtle as tg

def koch(lung, liv):
    if liv == 0: t.forward(lung); return
    koch(lung / 3.0, liv - 1)
    tina.left(60)
    koch(lung / 3.0, liv - 1)
    tina.right(120)
    koch(lung / 3.0, liv - 1)
    tina.left(60)
    koch(lung / 3.0, liv - 1)

fron pyturtle import *

piano = tg.TurtlePlane()
tina = tg.Turtle(x=-100)
koch(200, 4)
piano.mainloop()

Comportandosi come un segmento, possiamo utilizzare koch per realizzare un poligono, un triangolo con lato frattale:

...

def fiocco(lato, liv):
    for i in range(3):
        koch(lato, liv)
        tina.right(120)

...

fiocco(200, 4)

Molto regolare, ma se volessi introdurre un elemento di casualità? Ad esempio potremmo produrre la protuberanza a destra o a sinistra rispetto Tartaruga. E con questo realizzare un fiocco casuale.

import pygraph.pyturtle as tg
import random

def kochcas(lung, liv):
    if liv == 0:
        tina.forward(lung)
        return
    verso = random.randrange(-1, 2, 2)    # dà come risultato -1 o +1
    kochcas(lung / 3.0, liv - 1)
    tina.left(60 * verso)
    koch(lung / 3.0, liv - 1)
    tina.right(120 * verso)
    kochcas(lung / 3.0, liv - 1)
    tina.left(60 * verso)
    koch(lung / 3.0, liv - 1)

def fioccocas(lato, liv):
    for i in range(3):
        kochcas(lato, liv)
        tina.right(120)

piano = tg.TurtlePlane()
tina = tg.Turtle()
fioccocas(200, 4)
piano.mainloop()

Riassumendo¶

Una funzione si dice ricorsiva quando chiama sé stessa.
Perché una funzione ricorsiva sia utilizzabile all’interno di un programma, deve avere una condizione di terminazione, di solito posta all’inizio.
Una funzione ricorsiva si dice terminale se la chiamata ricorsiva non è seguita da altre istruzioni.
Le funzioni ricorsive terminali possono essere sostituite facilmente da cicli.
Le funzioni ricorsive non terminali hanno un comportamento che spesso è sorprendente.
Le funzioni ricorsive avvicinano i linguaggi procedurali a quelli dichiarativi. Infatti la domanda che si pone il programmatore per realizzare una funzione ricorsiva non è: “come si fa a fare…?”, ma: “cosa è …?”.